Object detection is all about drawing boxes (called bounding boxes) around objects of interest in a picture (see figure 12.1). This enables you to know not just which objects are in a picture, but also where they are. Some of its most common applications are
- Counting — Find out how many instances of an object are in an image.
- Tracking — Track how objects move in a scene over time by performing object detection on every frame of a movie.
- Cropping — Identify the area of an image that contains an object of interest to crop it and send a higher-resolution version of the image patch to a classifier or an Optical Character Recognition (OCR) model.

You might be thinking, if I have a segmentation mask for an object instance, I can already compute the coordinates of the smallest box that contains the mask. So couldn’t we just use image segmentation all the time? Do we need object detection models at all?
Indeed, segmentation is a strict superset of detection. It returns all the information that could be returned by a detection model — plus a lot more. This increased wealth of information has a significant computational cost: a good object detection model will typically run much faster than an image segmentation model. It also has a data labeling cost: to train a segmentation model, you need to collect pixel-precise masks, which are much more time-consuming to produce than the mere bounding boxes required by object detection models.
As a result, you will always want to use an object detection model if you have no need for pixel-level information — for instance, if all you want is to count objects in an image.
Single-stage vs. two-stage object detectors
There are two broad categories of object detection architectures:
- Two-stage detectors, which first extract region proposals, known as Region-based Convolutional Neural Networks (R-CNN) models
- Single-stage detectors, such as RetinaNet or the You Only Look Once family of models
Here’s how they work.
Two-stage R-CNN detectors
A region-based ConvNet, or R-CNN model, is a two-stage model. The first stage takes an image and produces a few thousand partially overlapping bounding boxes around areas that look object-like. These boxes are called region proposals. This stage isn’t very smart, so at that point we aren’t quite sure whether the proposed regions do contain objects and, if so, what objects they contain.
That’s the job of the second stage — a ConvNet that looks at each region proposal and classifies it into a number of predetermined classes, just like the models you’ve seen in chapter 9 (see figure 12.2). Region proposals that have a low score across all classes considered are discarded. We are then left with a much smaller set of boxes, each with a high class-presence score for one particular class. Finally, bounding boxes around each object are further refined to eliminate duplicates and make each bounding box as precise as possible.
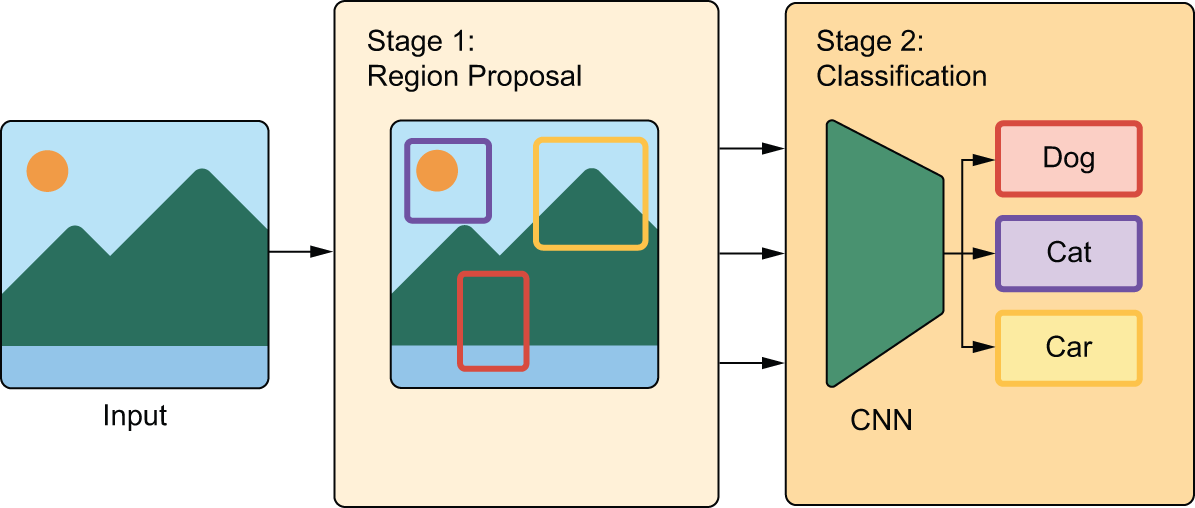
In early R-CNN versions, the first stage was a heuristic model called Selective Search that used some definition of spatial consistency to identify object-like areas. Heuristic is a term you’ll hear quite a lot in machine learning — it simply means “a bundle of hard-coded rules someone made up.” It’s usually used in opposition to learned models (where the rules are automatically derived) or theory-derived models. In later versions of R-CNN, such as Faster-R-CNN, the box generation stage became a deep learning model, called a Region Proposal Network.
The two-stage approach of R-CNN works very well in practice, but it’s quite computationally expensive, most notably because it requires you to classify thousands of patches — for every single image you process. That makes it unsuitable for most real-time applications and for embedded systems. My take is that, in practical applications, you generally don’t ever need a computationally expensive object detection system like R-CNN because if you’re doing server-side inference with a beefy GPU, then you’ll probably be better off using a segmentation model instead, like the Segment Anything model we saw in the previous chapter. And if you’re resource-constrained, then you’re going to want to use a more computationally efficient object detection architecture — a single-stage detector.
Single-stage detectors
Around 2015, researchers and practitioners began experimenting with using a single deep learning model to jointly predict bounding box coordinates together with their labels, an architecture called a single-stage detector. The main families of single-stage detectors are RetinaNet, Single Shot MultiBox Detectors (SSD), and the You Only Look Once family, abbreviated as YOLO. Yes, like the meme. That’s on purpose.
Single-stage detectors, especially recent YOLO iterations, boast significantly faster speeds and greater efficiency than their two-stage counterparts, albeit with a minor potential tradeoff in accuracy. Nowadays, YOLO is arguably the most popular object detection model out there, especially when it comes to real-time applications. There are usually a new version of it that comes out every year — interestingly, each new version tends to be developed by a separate organization.
In the next section, we will build a simplified YOLO model from scratch.
Training a YOLO model from scratch
Overall, building an object detector can be a bit of an undertaking — not that there’s anything theoretically complex about it. There’s just a lot of code needed to handle manipulating bounding boxes and predicted output. To keep things simple, we will recreate the very first YOLO model from 2015. There’s 12 YOLO versions as of this writing, but the original is a bit simpler to work with.
Downloading the COCO dataset
Before we start creating our model, we need data to train with. The COCO dataset [1], short for Common Objects in Context, is one of the best-known and most commonly used object detection datasets. It consists of real-world photos from a number of different sources plus human-created annotations. This includes object labels, bounding box annotations, and full segmentation masks. We will disregard the segmentation masks and just use bounding boxes.
Let’s download the 2017 version of the COCO dataset. While not a large dataset by today’s standards, this 18 GB dataset will be the largest dataset we use in the book. If you are running the code as you read, this is a good chance to take a breather.
import keras
import keras_hub
images_path = keras.utils.get_file(
"coco",
"http://images.cocodataset.org/zips/train2017.zip",
extract=True,
)
annotations_path = keras.utils.get_file(
"annotations",
"http://images.cocodataset.org/annotations/annotations_trainval2017.zip",
extract=True,
)
We need to do some input massaging before we are ready to use this data. The first download gives us an unlabeled directory of all the COCO images. The second download includes all image metadata via a JSON file. COCO associates each image file with an ID, and each bounding box is paired with one of these IDs. We need to collate all box and image data together.
Each bounding box comes with x, y, width, height pixel coordinates starting at
the top left corner of the image. As we load our data, we can rescale all
bounding box coordinates so they are points in a [0, 1] unit square. This will
make it easier to manipulate these boxes without needing to check the size of
each input image.
import json
with open(f"{annotations_path}/annotations/instances_train2017.json", "r") as f:
annotations = json.load(f)
# Sorts image metadata by ID
images = {image["id"]: image for image in annotations["images"]}
# Converts bounding box to coordinates on a unit square
def scale_box(box, width, height):
scale = 1.0 / max(width, height)
x, y, w, h = [v * scale for v in box]
x += (height - width) * scale / 2 if height > width else 0
y += (width - height) * scale / 2 if width > height else 0
return [x, y, w, h]
# Aggregates all bounding box annotations by image ID
metadata = {}
for annotation in annotations["annotations"]:
id = annotation["image_id"]
if id not in metadata:
metadata[id] = {"boxes": [], "labels": []}
image = images[id]
box = scale_box(annotation["bbox"], image["width"], image["height"])
metadata[id]["boxes"].append(box)
metadata[id]["labels"].append(annotation["category_id"])
metadata[id]["path"] = images_path + "/train2017/" + image["file_name"]
metadata = list(metadata.values())
Let’s take a look at the data we just loaded.
>>> len(metadata)117266>>> min([len(x["boxes"]) for x in metadata])1>>> max([len(x["boxes"]) for x in metadata])63>>> max(max(x["labels"]) for x in metadata) + 191>>> metadata[435]{"boxes": [[0.12, 0.27, 0.57, 0.33], [0.0, 0.15, 0.79, 0.69], [0.0, 0.12, 1.0, 0.75]], "labels": [17, 15, 2], "path": "/root/.keras/datasets/coco/train2017/000000171809.jpg"}>>> [keras_hub.utils.coco_id_to_name(x) for x in metadata[435]["labels"]]["cat", "bench", "bicycle"]
We have 117,266 images. Each image can have anywhere from 1 to 63 objects with an associated bounding box. There are only 91 possible labels for objects, chosen by the COCO dataset creators.
We can use a KerasHub utility keras_hub.utils.coco_id_to_name(id) to map
these integer labels to human-readable names, similar to the utility
we used to decode ImageNet predictions to text labels back in chapter 8.
Let’s visualize an example image to make this a little more concrete. We can define a function to draw an image with Matplotlib and another function to draw a labeled bounding box on this image. We will need both of these throughout the chapter. We can use the HSV colorspace as a simple trick to generate new colors for each new label we see. By fixing the saturation and brightness of the color and only updating its hue, we can generate bright new colors that stand out clearly from our image.
import matplotlib.pyplot as plt
from matplotlib.colors import hsv_to_rgb
from matplotlib.patches import Rectangle
color_map = {0: "gray"}
def label_to_color(label):
# Uses the golden ratio to generate new hues of a bright color with
# the HSV colorspace
if label not in color_map:
h, s, v = (len(color_map) * 0.618) % 1, 0.5, 0.9
color_map[label] = hsv_to_rgb((h, s, v))
return color_map[label]
def draw_box(ax, box, text, color):
x, y, w, h = box
ax.add_patch(Rectangle((x, y), w, h, lw=2, ec=color, fc="none"))
textbox = dict(fc=color, pad=1, ec="none")
ax.text(x, y, text, c="white", size=10, va="bottom", bbox=textbox)
def draw_image(ax, image):
# Draws the image on a unit cube with (0, 0) at the top left
ax.set(xlim=(0, 1), ylim=(1, 0), xticks=[], yticks=[], aspect="equal")
image = plt.imread(image)
height, width = image.shape[:2]
# Pads the image so it fits inside the unit cube
hpad = (1 - height / width) / 2 if width > height else 0
wpad = (1 - width / height) / 2 if height > width else 0
extent = [wpad, 1 - wpad, 1 - hpad, hpad]
ax.imshow(image, extent=extent)
Let’s use our new visualization to look at the sample image[2] we were inspecting earlier (see figure 12.3):
sample = metadata[435]
ig, ax = plt.subplots(dpi=300)
draw_image(ax, sample["path"])
for box, label in zip(sample["boxes"], sample["labels"]):
label_name = keras_hub.utils.coco_id_to_name(label)
draw_box(ax, box, label_name, label_to_color(label))
plt.show()

While it would be fun to train on all 18 gigabytes of our input data, we want to keep the examples in this book easily runnable on modest hardware. If we limit ourselves to only images with four or fewer boxes, we will make our training problem easier and a halve the data size. Let’s do this and shuffle our data — the images are grouped by object type, which would be terrible for training:
import random
metadata = list(filter(lambda x: len(x["boxes"]) <= 4, metadata))
random.shuffle(metadata)
That’s it for data loading! Let’s start creating our YOLO model.
Creating a YOLO model
As mentioned previously, the YOLO model is a single stage detector. Rather than first attempting to identify all candidate objects in a scene and then classifying the object regions, YOLO will propose bounding boxes and object labels in one go.
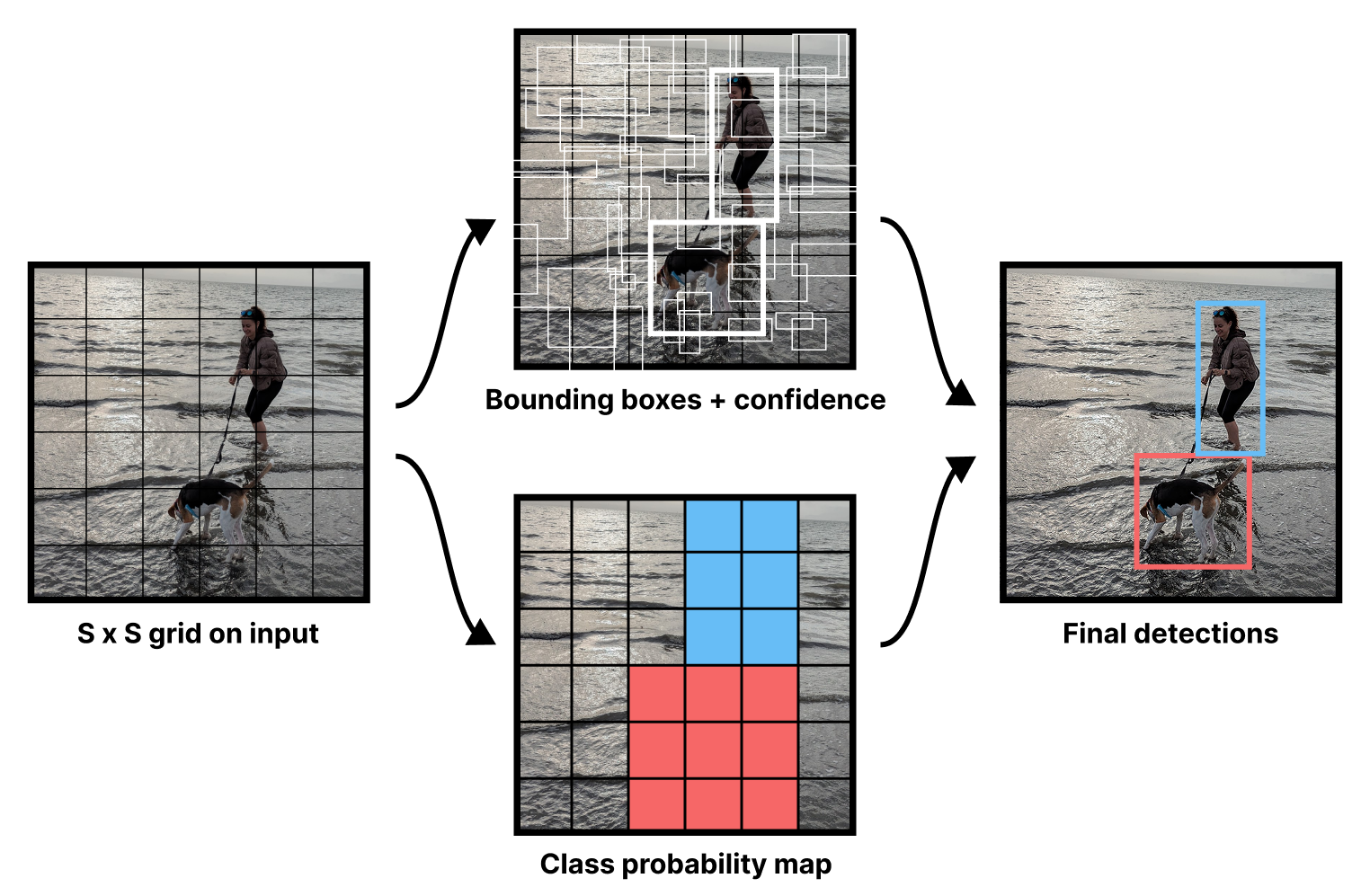
Our model will divide an image up into a grid and predict two separate outputs at each grid location — a bounding box and a class label. In the original paper by Redmon et al.[3], the model actually predicted multiple boxes per grid location, but we keep things simple and just predict one box in each grid square.
Most images will not have objects evenly distributed across a grid, and to account for this, the model will output a confidence score along with each box, as shown in figure 12.4. We’d like this confidence to be high when an object is detected at a location, and zero when there’s no object. Most grid locations will have no object and should report a near-zero confidence.
Like many models in computer vision, the YOLO model uses a ConvNet backbone to obtain interesting high-level features for an input image, a concept we first explored in chapter 8. In their paper, the authors created their own backbone model and pretrained it with ImageNet for classification. Rather than do this ourselves, we can instead use KerasHub to load a pretrained backbone.
Instead of using the Xception backbone we’ve used so far in this book, we will switch to ResNet, a family of models we first mentioned in chapter 9. The structure is quite similar to Xception, but ResNet uses strides instead of pooling layers to downsample the image. As we mentioned in chapter 11, strided convolutions are better when we care about the spatial location of the input.
Let’s load up our pretrained model and matching preprocessing (to rescale the image). We will resize our images to 448 × 448; image input size is quite important for the object detection task.
image_size = 448
backbone = keras_hub.models.Backbone.from_preset(
"resnet_50_imagenet",
)
preprocessor = keras_hub.layers.ImageConverter.from_preset(
"resnet_50_imagenet",
image_size=(image_size, image_size),
)
Next, we can turn our backbone into a detection model by adding new layers for outputting box and class predictions. The setup proposed in the YOLO paper is quite simple. Take the output of a ConvNet backbone and feed it through two densely connected layers with an activation in the middle. Then, split the output. The first five numbers will be used for bounding box prediction (four for the box and one for the box confidence). The rest will be used for the class probability map shown in figure 12.4 — a classification prediction for each grid location over all possible 91 labels.
Let’s write this out.
from keras import layers
grid_size = 6
num_labels = 91
inputs = keras.Input(shape=(image_size, image_size, 3))
x = backbone(inputs)
# Makes our backbone outputs smaller and then flattens the output
# features
x = layers.Conv2D(512, (3, 3), strides=(2, 2))(x)
x = keras.layers.Flatten()(x)
# Passes our flattened feature maps through two densely connected
# layers
x = layers.Dense(2048, activation="relu", kernel_initializer="glorot_normal")(x)
x = layers.Dropout(0.5)(x)
x = layers.Dense(grid_size * grid_size * (num_labels + 5))(x)
# Reshapes outputs to a 6 × 6 grid
x = layers.Reshape((grid_size, grid_size, num_labels + 5))(x)
# Split box and class predictions
box_predictions = x[..., :5]
class_predictions = layers.Activation("softmax")(x[..., 5:])
outputs = {"box": box_predictions, "class": class_predictions}
model = keras.Model(inputs, outputs)
We can get a better sense of the model by looking at the model summary:
>>> model.summary()Model: "functional_3" ┏━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━┩ │ input_layer_7 │ (None, 448, 448, │ 0 │ - │ │ (InputLayer) │ 3) │ │ │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ res_net_backbone_12 │ (None, 14, 14, │ 23,580,512 │ input_layer_7[0][… │ │ (ResNetBackbone) │ 2048) │ │ │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ conv2d_3 (Conv2D) │ (None, 6, 6, 512) │ 9,437,696 │ res_net_backbone_… │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ flatten_3 (Flatten) │ (None, 18432) │ 0 │ conv2d_3[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ dense_6 (Dense) │ (None, 2048) │ 37,750,784 │ flatten_3[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ dropout_3 (Dropout) │ (None, 2048) │ 0 │ dense_6[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ dense_7 (Dense) │ (None, 3456) │ 7,081,344 │ dropout_3[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ reshape_3 (Reshape) │ (None, 6, 6, 96) │ 0 │ dense_7[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ get_item_7 (GetItem) │ (None, 6, 6, 91) │ 0 │ reshape_3[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ get_item_6 (GetItem) │ (None, 6, 6, 5) │ 0 │ reshape_3[0][0] │ ├───────────────────────┼───────────────────┼─────────────┼────────────────────┤ │ activation_33 │ (None, 6, 6, 91) │ 0 │ get_item_7[0][0] │ │ (Activation) │ │ │ │ └───────────────────────┴───────────────────┴─────────────┴────────────────────┘ Total params: 77,850,336 (296.98 MB) Trainable params: 77,797,088 (296.77 MB) Non-trainable params: 53,248 (208.00 KB)
Our backbone outputs have shape (batch_size, 14, 14, 2048). That is 401,408
output floats per image, a bit too many to feed into our dense layers. We
downscale the feature maps with a strided conv layer to
(batch_size, 6, 6, 512) with a more manageable 18,432 floats per image.
Next, we can add our two densely connected layers. We flatten the entire feature
map, pass it through a Dense with a relu activation and then pass it through a
final Dense with our exact number of output predictions — 5 for the bounding
box and confidence and 91 for each object class at each grid location.
Finally, we reshape the outputs back to a 6 × 6 grid and split our box and class predictions. As usual for our classification outputs, we apply a softmax. The box outputs will need more special consideration; we will cover this later.
Looking good! Note that because we flatten the entire feature map through the classification layer, every grid detector can use the entire image’s features; there’s no locality constraint. This is by design — large objects will not stay contained to a single grid cell.
Readying the COCO data for the YOLO model
Our model is relatively simple, but we still need to preprocess our inputs to
align them with the prediction grid. Each grid detector will be responsible for
detecting any boxes whose center falls inside the grid box. Our model will
output five floats for the box (x, y, w, h, confidence). The x and y will
represent the object’s center relative to the bounds of the grid cell (from 0 to
1). The w and h will represent the object’s size relative to the image size.
We already have the right w and h values in our training data. However, we
need to translate our x and y values to and from the grid. Let’s define two
utilities:
def to_grid(box):
x, y, w, h = box
cx, cy = (x + w / 2) * grid_size, (y + h / 2) * grid_size
ix, iy = int(cx), int(cy)
return (ix, iy), (cx - ix, cy - iy, w, h)
def from_grid(loc, box):
(xi, yi), (x, y, w, h) = loc, box
x = (xi + x) / grid_size - w / 2
y = (yi + y) / grid_size - h / 2
return (x, y, w, h)
Let’s rework our training data so it conforms to this new grid structure. We can create two arrays as long as our dataset with our grid:
- The first will contain our class probability map. We will mark all grid cells that intersect with a bounding box with the correct label. To keep our code simple, we won’t worry about overlapping boxes.
- The second will contain the boxes themselves. We will translate all boxes to the grid and label the correct grid cell with the coordinates for the box. The confidence for an actual box in our label data will always be one, and the confidence for all other locations will be zero.
import numpy as np
import math
class_array = np.zeros((len(metadata), grid_size, grid_size))
box_array = np.zeros((len(metadata), grid_size, grid_size, 5))
for index, sample in enumerate(metadata):
boxes, labels = sample["boxes"], sample["labels"]
for box, label in zip(boxes, labels):
(x, y, w, h) = box
# Finds all grid cells whose center falls inside the box
left, right = math.floor(x * grid_size), math.ceil((x + w) * grid_size)
bottom, top = math.floor(y * grid_size), math.ceil((y + h) * grid_size)
class_array[index, bottom:top, left:right] = label
for index, sample in enumerate(metadata):
boxes, labels = sample["boxes"], sample["labels"]
for box, label in zip(boxes, labels):
# Transforms the box to the grid coordinate system
(xi, yi), (grid_box) = to_grid(box)
box_array[index, yi, xi] = [*grid_box, 1.0]
# Makes sure the class label for the box's center location
# matches the box
class_array[index, yi, xi] = label
Let’s visualize our YOLO training data with our box drawing helpers (figure 12.5). We will draw the entire class activation map over our first input image[4] and add the confidence score of a box along with its label.
def draw_prediction(image, boxes, classes, cutoff=None):
fig, ax = plt.subplots(dpi=300)
draw_image(ax, image)
# Draws the YOLO output grid and class probability map
for yi, row in enumerate(classes):
for xi, label in enumerate(row):
color = label_to_color(label) if label else "none"
x, y, w, h = (v / grid_size for v in (xi, yi, 1.0, 1.0))
r = Rectangle((x, y), w, h, lw=2, ec="black", fc=color, alpha=0.5)
ax.add_patch(r)
# Draws all boxes at each grid location above our cutoff
for yi, row in enumerate(boxes):
for xi, box in enumerate(row):
box, confidence = box[:4], box[4]
if not cutoff or confidence >= cutoff:
box = from_grid((xi, yi), box)
label = classes[yi, xi]
color = label_to_color(label)
name = keras_hub.utils.coco_id_to_name(label)
draw_box(ax, box, f"{name} {max(confidence, 0):.2f}", color)
plt.show()
draw_prediction(metadata[0]["path"], box_array[0], class_array[0], cutoff=1.0)

Lastly, let’s use tf.data to load our image data. We will load our images
from disk, apply our preprocessing, and batch them. We should also split a
validation set to monitor training.
import tensorflow as tf
# Loads and resizes the model with tf.data
def load_image(path):
x = tf.io.read_file(path)
x = tf.image.decode_jpeg(x, channels=3)
return preprocessor(x)
images = tf.data.Dataset.from_tensor_slices([x["path"] for x in metadata])
images = images.map(load_image, num_parallel_calls=8)
labels = {"box": box_array, "class": class_array}
labels = tf.data.Dataset.from_tensor_slices(labels)
# Creates a merged dataset and batches it
dataset = tf.data.Dataset.zip(images, labels).batch(16).prefetch(2)
# Splits off some validation data
val_dataset, train_dataset = dataset.take(500), dataset.skip(500)
With that, our data is ready for training.
Training the YOLO model
We have our model and our training data ready, but there’s one last element we
need before we can actually run fit(): the loss function. Our model outputs
predicted boxes and predicted grid labels. We saw in chapter 7 how we can define
multiple losses for each output — Keras will simply sum the losses together
during training. We can handle the classification loss with
sparse_categorical_crossentropy as usual.
The box loss, however, needs some special consideration. The basic loss proposed by the YOLO authors is fairly simple. They use the sum-squared error of the difference between the target box parameters and the predicted ones. We will only compute this error for grid cells with actual boxes in the labeled data.
The tricky part of the loss is the box confidence output. The authors wanted the confidence output to reflect not just the presence of an object, but also how good the predicted box is. To create a smooth estimate of how good a box prediction is, the authors propose using the Intersection over Union (IoU) metric we saw last chapter. If a grid cell is empty, the predicted confidence at the location should be zero. However, if a grid cell contains an object, we can use the IoU score between the current box prediction and the actual box as the target confidence value. This way, as the model becomes better at predicting box locations, the IoU score and the learned confidence values will go up.
This calls for a custom loss function. We can start be defining a utility to compute IoU scores for target and predicted boxes.
from keras import ops
# Unpacks a tensor of boxes
def unpack(box):
return box[..., 0], box[..., 1], box[..., 2], box[..., 3]
# Computes the intersection area between two box tensors
def intersection(box1, box2):
cx1, cy1, w1, h1 = unpack(box1)
cx2, cy2, w2, h2 = unpack(box2)
left = ops.maximum(cx1 - w1 / 2, cx2 - w2 / 2)
bottom = ops.maximum(cy1 - h1 / 2, cy2 - h2 / 2)
right = ops.minimum(cx1 + w1 / 2, cx2 + w2 / 2)
top = ops.minimum(cy1 + h1 / 2, cy2 + h2 / 2)
return ops.maximum(0.0, right - left) * ops.maximum(0.0, top - bottom)
# Computes the IoU between two box tensors
def intersection_over_union(box1, box2):
cx1, cy1, w1, h1 = unpack(box1)
cx2, cy2, w2, h2 = unpack(box2)
intersection_area = intersection(box1, box2)
a1 = ops.maximum(w1, 0.0) * ops.maximum(h1, 0.0)
a2 = ops.maximum(w2, 0.0) * ops.maximum(h2, 0.0)
union_area = a1 + a2 - intersection_area
return ops.divide_no_nan(intersection_area, union_area)
Let’s use this utility to define our custom loss. Redmon et al. propose a couple of loss scaling tricks to improve the quality of training:
- They scale up the box placement loss by a factor of five, so it becomes a more important part of overall training.
- Since most grid cells are empty, they also scale down the confidence loss in empty locations by a factor of two. This keeps these zero confidence predictions from overwhelming the loss.
- They take the square root of the width and height before computing the
loss. This is to stop large boxes from mattering disproportionately more than
small boxes. We will use a
sqrtfunction that preserves the sign of the input, since our model might predict negative widths and heights at the start of training.
Let’s write this out.
def signed_sqrt(x):
return ops.sign(x) * ops.sqrt(ops.absolute(x) + keras.config.epsilon())
def box_loss(true, pred):
# Unpacks values
xy_true, wh_true, conf_true = true[..., :2], true[..., 2:4], true[..., 4:]
xy_pred, wh_pred, conf_pred = pred[..., :2], pred[..., 2:4], pred[..., 4:]
# If confidence_true is 0.0, there is no object in this grid cell.
no_object = conf_true == 0.0
# Computes box placement errors
xy_error = ops.square(xy_true - xy_pred)
wh_error = ops.square(signed_sqrt(wh_true) - signed_sqrt(wh_pred))
# Computes confidence error
iou = intersection_over_union(true, pred)
conf_target = ops.where(no_object, 0.0, ops.expand_dims(iou, -1))
conf_error = ops.square(conf_target - conf_pred)
# Concatenates the errors weith scaling hacks
error = ops.concatenate(
(
ops.where(no_object, 0.0, xy_error * 5.0),
ops.where(no_object, 0.0, wh_error * 5.0),
ops.where(no_object, conf_error * 0.5, conf_error),
),
axis=-1,
)
# Returns one loss value per sample; Keras will sum over the batch.
return ops.sum(error, axis=(1, 2, 3))
We are finally ready to start training our YOLO model. Purely to keep this example short, we will skip over metrics. In a real-world setting, you’d want quite a few metrics here — such as the accuracy of the model at different confidence cutoff levels.
model.compile(
optimizer=keras.optimizers.Adam(2e-4),
loss={"box": box_loss, "class": "sparse_categorical_crossentropy"},
)
model.fit(
train_dataset,
validation_data=val_dataset,
epochs=4,
)
Training takes over an hour on the Colab free GPU runtime, and our model is still undertrained (validation loss is still falling!). Let’s try visualizing an output from our model (figure 12.6). We will use a low-confidence cutoff, as our model is not a very good object detector quite yet.
# Rebatches our dataset to get a single sample instead of 16
x, y = next(iter(val_dataset.rebatch(1)))
preds = model.predict(x)
boxes = preds["box"][0]
# Uses argmax to find the most likely label at each grid location
classes = np.argmax(preds["class"][0], axis=-1)
# Loads the image from disk to view it a full size
path = metadata[0]["path"]
draw_prediction(path, boxes, classes, cutoff=0.1)

We can see our model is starting to understand box locations and class labels, though it is still not very accurate. Let’s visualize every box predicted by the model (figure 12.7), even those with zero confidence:
draw_prediction(path, boxes, classes, cutoff=None)
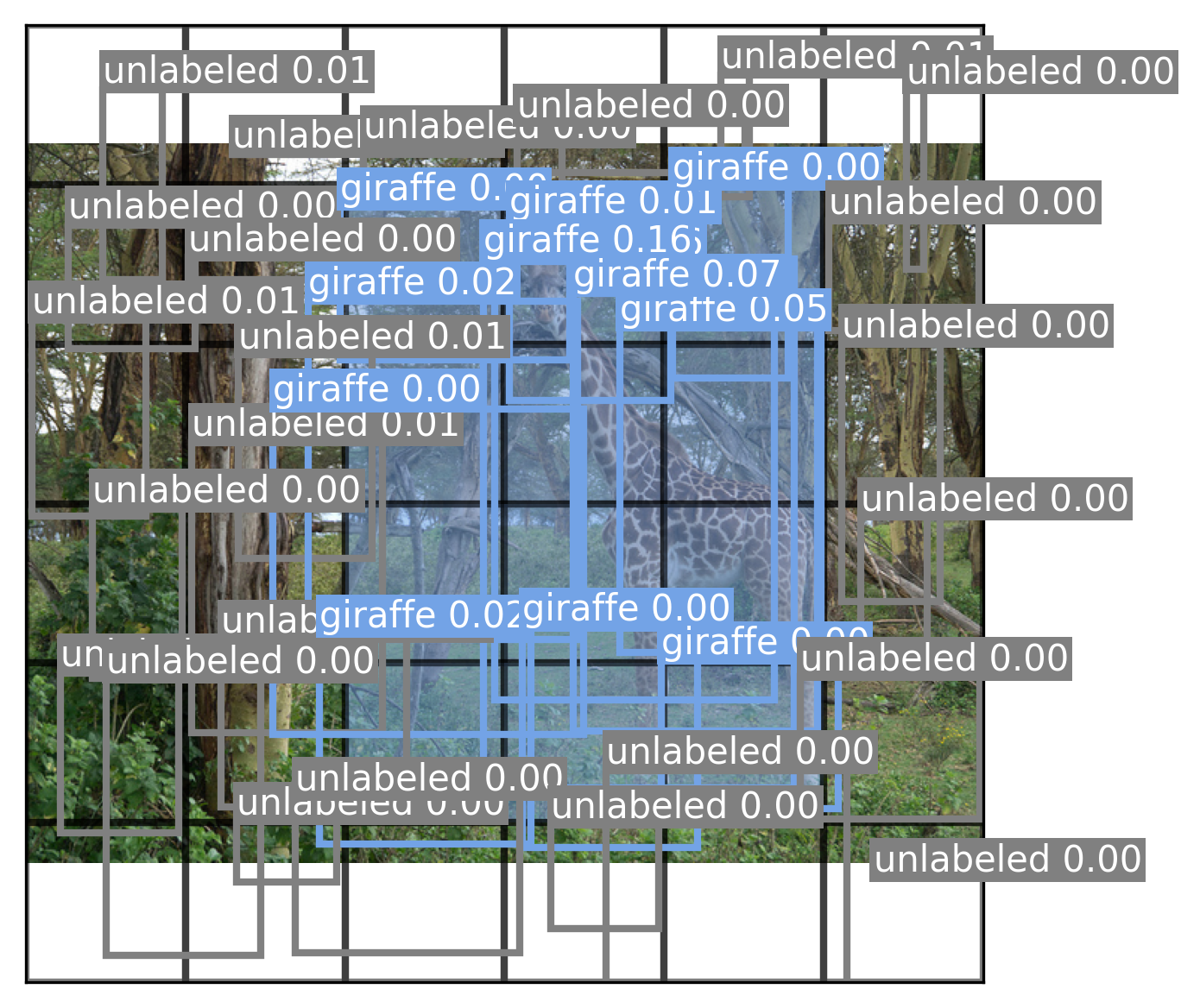
Our model learns very low-confidence values because it has not yet learned to consistently locate objects in a scene. To further improve the model, we should try a number of things:
- Train for more epochs
- Use the whole COCO dataset
- Data augmentation (e.g., translating and rotating input images and boxes)
- Improve our class probability map for overlapping boxes
- Predict multiple boxes per grid location using a bigger output grid
All of these would positively affect the model performance and get us closer to the original YOLO training recipe. However, this example is really just to get a feel for object detection training — training an accurate COCO detection model from scratch would take a large amount of compute and time. Instead, to get a sense of a better-performing detection model, let’s try using a pretrained object detection model called RetinaNet.
Using a pretrained RetinaNet detector
RetinaNet is also a single-stage object detector and operates on the same basic principles as the YOLO model. The biggest conceptual difference between our model and RetinaNet is that RetinaNet uses its underlying ConvNet differently to better handle both small and large objects simultaneously.
In our YOLO model, we simply took the final outputs of our ConvNet and used them to build our object detector. These output features map to large areas on our input image — as a result, they are not very effective at finding small objects in the scene.
One option to solve this scale issue would be to directly use the output of earlier layers in our ConvNet. This would extract high-resolution features that map to small localized areas of our input image. However, the output of these early layers is not very semantically interesting. It might map to different types of simple features like edges and curves, but only later in the ConvNet layers do we start building latent representations for entire objects.
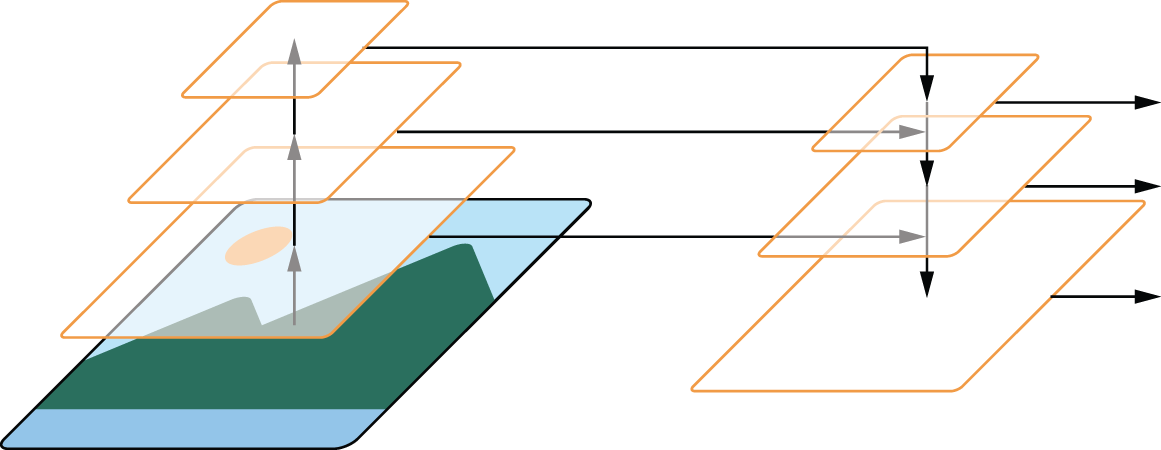
The solution used by RetinaNet is called a feature pyramid network. The final
features from the ConvNet base model are upsampled with progressive
Conv2DTranspose layers, just like we saw in the previous chapter. But critically, we also
include lateral connections where we sum these upsampled feature maps with the
feature maps of the same size from the original ConvNet. This combines the
semantically interesting, low-resolution features at the end of the ConvNet with
the high-resolution, small-scale features from the beginning of the ConvNet. A
rough sketch of this architecture is shown in figure 12.8.
Feature pyramid networks can substantially boost performance by building effective features for both small and large objects in terms of pixel footprint. Recent versions of YOLO also use the same setup.
Let’s go ahead and try out the RetinaNet model, which was also trained on the COCO dataset. To make this a little more interesting, let’s try an image that is out-of-distribution for the model, the Pointillist painting A Sunday Afternoon on the Island of La Grande Jatte.
We can start by downloading the image and converting it to a NumPy array:
url = "https://s3.us-east-1.amazonaws.com/book.keras.io/3e/seurat.jpg"
path = keras.utils.get_file(origin=url)
image = np.array([keras.utils.load_img(path)])
Next, let’s download the model and make a prediction. As we did in the previous chapter,
we can use the high-level task API in KerasHub to create an ObjectDetector
and use it — preprocessing included.
detector = keras_hub.models.ObjectDetector.from_preset(
"retinanet_resnet50_fpn_v2_coco",
bounding_box_format="rel_xywh",
)
predictions = detector.predict(image)
You’ll note we pass an extra argument to specify the bounding box format. We can
do this for most Keras models and layers that support bounding boxes. We pass
"rel_xywh" to use the same format as we did for the YOLO model, so we can use
the same box-drawing utilities. Here, rel stands for relative to the image
size (e.g., from [0, 1]). Let’s inspect the prediction we just made:
>>> [(k, v.shape) for k, v in predictions.items()][("boxes", (1, 100, 4)), ("confidence", (1, 100)), ("labels", (1, 100)), ("num_detections", (1,))]>>> predictions["boxes"][0][0]array([0.53, 0.00, 0.81, 0.29], dtype=float32)
We have four different model outputs: bounding boxes, confidences, labels, and the total number of detections. This is overall quite similar to our YOLO model. The model can predict a total of 100 objects for each input model.
Let’s try displaying the prediction with our box drawing utilities (figure 12.9).
fig, ax = plt.subplots(dpi=300)
draw_image(ax, path)
num_detections = predictions["num_detections"][0]
for i in range(num_detections):
box = predictions["boxes"][0][i]
label = predictions["labels"][0][i]
label_name = keras_hub.utils.coco_id_to_name(label)
draw_box(ax, box, label_name, label_to_color(label))
plt.show()
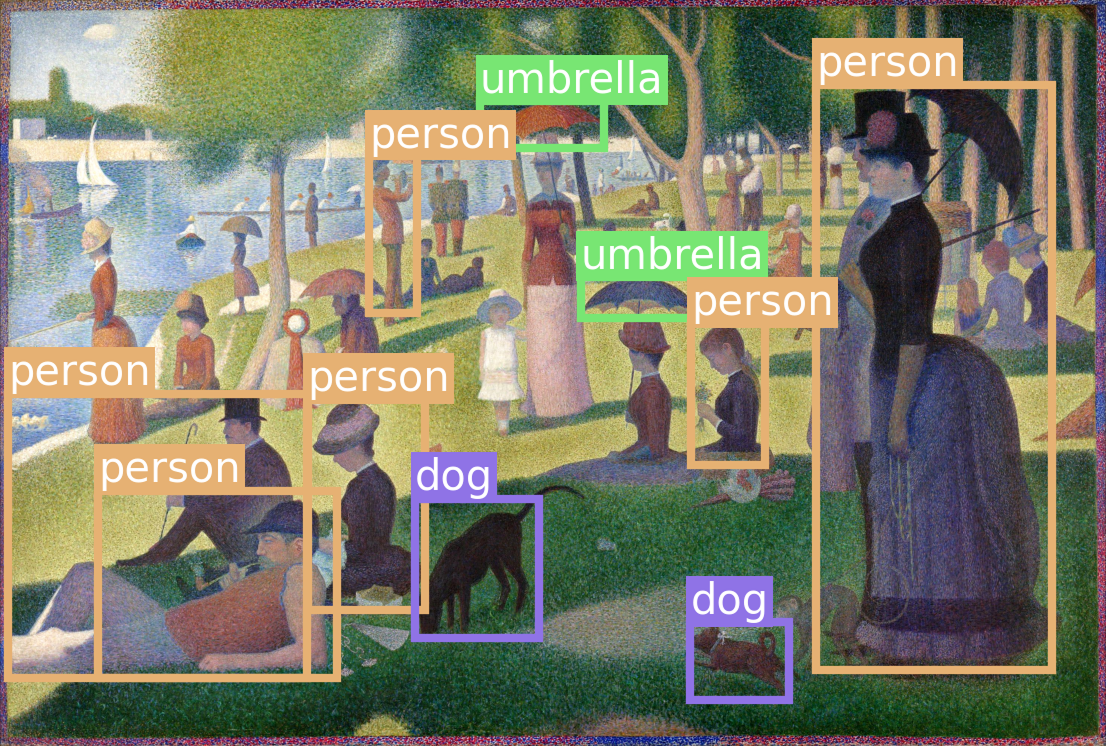
The RetinaNet model is able to generalize to a pointillist painting with ease, despite no training on this style of input! This is actually one of the advantages of single-stage object detectors. Paintings and photographs are very different at a pixel level but share a similar structure at a high level. Two-stage detectors like R-CNNs, in contrast, are forced to classify small patches of an input image in isolation, which is extra difficult when small patches of pixels look very different than training data. Single-stage detectors can draw on features from the entire input and are more robust to novel test-time inputs.
With that, you have reached the end of the computer vision section of this book! We have trained image classifiers, segmenters, and object detectors from scratch. We’ve developed a good intuition for how ConvNets work, the first major success of the deep learning era. We aren’t quite done with images yet; you will see them again in chapter 17 when we start generating image output.
Summary
- Object detection identifies and locates objects within an image using bounding boxes. It’s basically a weaker version of image segmentation, but one that can be run much more efficiently.
- There are two primary approaches to object detection:
- Region-based Convolutional Neural Networks (R-CNNs), which are two-stage models that first propose regions of interest and then classify them with a ConvNet.
- Single-stage detectors (like RetinaNet and YOLO), which perform both tasks in a single step. Single-stage detectors are generally faster and more efficient, making them suitable for real-time applications (e.g., self-driving cars).
- YOLO computes two separate outputs simultaneously during training
— possible bounding boxes and a class probability map:
- Each candidate bounding box is paired with a confidence score, which is trained to target the Intersection over Union of the predicted box and the ground truth box.
- The class probability map classifies different regions of an image as belonging to different objects.
- RetinaNet builds on this idea by using a feature pyramid network (FPN), which combines features from multiple ConvNet layers to create feature maps at different scales, allowing it to more accurately detect objects of different sizes.



